 Fear
Fear
29 - 31 May - and some stuff about counting
A couple of nights back after we'd retired to bed
we were kept awake by the sound of singing or drumming from somewhere very close
to the house; "very close" here meaning either right outside or on the next roof
terrace or both. Paula went downstairs and I lay in bed knowing that she was
capable of going outside and telling them all to shut up, and quietly hoping
that she wouldn't. Well, she shut the window and banged on it meaningfully a
couple of times, and immediately
the drums were joined by louder drums
augmented with a front line of the type of trumpet that they have round here.
Since it's unlikely that they had spare armed musicians on stand-by in case
anyone cut up rough this was almost certainly a coincidence. But the music was
very loud and there was a brief instant when I had to remind myself that it
wasn't threatening - a little like when lions were padding right by our car and
I had to resist a momentary impulse to close the window. In this instance I
ascribe the moment of fear to the fact that pretty much every person I've seen
photographed in the UK press and identified as Arabic over the past few years
had some connection with brutal acts of terrorism. In contrast, the people
we've actually met here have all been really friendly. In reality, the noise was
in all likelihood a festivity associated with a birth or a circumcision or some
other event that's happily celebrated here. At about 1 am I peeked out of the
window and saw girls as young as three or four hanging out with older women;
within about half an hour it was all
over.
Another topic for which people can cultivate a fear is maths. Yesterday I had a very interesting email from my friend Steve Mildenhall in response to my entry about Andrew Wiles etc. (Memories of the Blair Administration). In that blog I claimed that only a few people in the world were capable of understanding the proof of Fermat's Last Theorem. It turns out that Steve is one of them. This doesn't disprove my assertion, by the way: apart from being extremely smart and hard-working, Steve covered just the type of maths needed in his PhD - and was prepared to spend 3 months doing little other than reading the Wiles proof. In his email Steve noted that his all time favourite maths result is that you can't count the real numbers. One of the beauties of this result is that I can explain it to you.
"Count" means just what you'd expect: mathematicians reassuringly say that a set is countable if you can number the elements, starting with 1 then 2 and so forth. Key point is that you don't have to reach a number where you stop counting for the set to be countable - this describes infinite sets.
Let's put aside for a moment what "real" means here, and why you can't count the real numbers. There are plenty of sets of numbers that you can count. For example, the set of even numbers is countable: 2 is the first, 4 is the second, 6 is the third etc. The set of all positive and negative whole numbers (..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...) is called the integers. While you may think that there are twice as many of these as there are counting numbers (1, 2, 3 etc) it turns out that you can still count them. For example, you can go 0, 1, -1, 2, -2, 3, -3, 4, -4 etc. and every one of the integers will show up on the list that you make.
More surprisingly, the set of all numbers that you can write as a fraction - like 3/4 or 22/7 - is also countable, though this requires a bit more guile to show. First, you have to show a way to lay them all out. A good way way is to make a grid with the numerator (the number on the top of the fraction) along the y-axis and the denominator (the number at the bottom of the fraction) along the x-axis. Then every rational is given by one of the grid points.
Having laid the numbers out on a grid you can count them by starting in the corner and working outwards like this:
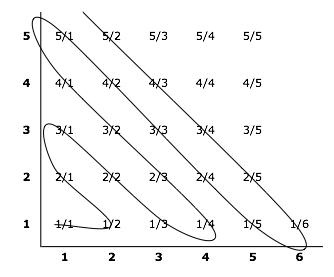
The squiggly line gives you the order in which you count the numbers onto your list (if it troubles you that some of these are equal - like 2/2 and 3/3 - you can skip over them after their first appearance).
Well you may wonder if there's anything that you can't count. There is. The numbers like those above that can be expressed as something over something else are called the rationals. In contrast, the entire set of numbers that can be expressed using decimal notation is called (for reasons that you'll be questioning by the end of this blog) the reals. Many people know that pi is an example of a number that can't be expressed precisely as a fraction - 22/7 being an approximation. It's easy to prove that the same is also true of the square root of two. (I wont do it because I'd need to use something that would start to look like an equation.) Now we get to the interesting argument that a mathematician called Cantor found to prove that the reals aren't countable, which runs as follows....
Let's suppose that someone claims that they did find a way to count the real numbers and got them into a list like we did for the evens and the integers. Just to make it concrete, lets assume that the first four numbers in the list are:
something.2451890...
something.7615208...
something.3212122...
something.8734261...
something.4545452...
Cantor pointed out that for any such list you can make another real number that isn't on. Start it with 0. and then set the first digit after the decimal place to be anything that isn't 2 (thus making it different from the first number on the list), the second digit after the decimal to be anything except 6 (thus making it different from the 2nd number), the 3rd digit after the decimal to anything except 1 (thus making it different from the 3rd number) etc etc. Carrying on with this ad infinitum ensures that the number you make isn't the same as any of the numbers on the list, and so the list can't cover all of the reals as claimed.
This is Steve's favourite result - I told you I could explain it! Many of Cantor's contemporaries thought that this was very fishy.
It shows that there's more than one kind of infinity and that in a sense the infinity of the reals (called aleph-1 by mathematicians) is "bigger" than the inifinity of the rationals (called aleph-0). The way that we say this while avoiding saying that one type of infinity is bigger than another (which could sound like nonsense) is to say that aleph-1 has greater cardinality than aleph-0. There is a continuity hypothesis that there aren't any infinities with cardinality between aleph-0 and aleph-1, but there is no known logical proof for this.
When I explained this to Zoe this afternoon (over mint tea and Sprite at the Nejjarine museum) I likened it to when you learn about monkeys: when you're young you know that monkeys are brown hairy animals that swing in the trees. Then when you get older you learn that monkeys come in vervet, squirrel, spider and other types. They all generally have the monkey characteristics that you first learned but there is more nuance than you first appreciated. Same with infinities.
The infinities higher than aleph-0 are really weird. There is a famous result with a geeky name (the Banach-Tarski paradox - Mike said I should mention it) that proves that you can take a "real" sphere, split it into 4 parts and a dot in the middle and then re-assemble it into two spheres each identical to the original. This provides a good hint that the reals aren't real.
Another sign of the weirdness of the reals is to try to find some? Probability tells us that if you pick a number at random on the number line it will, certainly, be a real that's not rational. However, you can easily show that the set of decimal-style numbers for which you can provide an algorithm to say how to determine which digit is at each place of the decimal expansion - or even the wider set of numbers for which you can give any sort of description - is countable. So the uncountability of aleph-1 is provided by numbers for which in principle there can be no description.
There's a lot more that could be said about this but for now I'll hint that the point where it goes funny is where you're allowed to keep making a free choice of the next digit ad infinitum...
Do you find all of this scary, boring or interesting?
This morning I went to get a paper and some vegetables, which is pretty much part of my daily routine, and wore my shorts in the medina for the first time. All the time I was out I didn't see another adult's knees and it felt really uncomfortable; shows how quickly you can fall into the small habits of cultural acclimation.
I read in the paper that the French have voted Non to the "constitution". I never would have expected that. The confusion into which Europe is now propelled will be entertaining and Corsica may be an interesting place from which to watch what happens next - we'll be there at the weekend.
Another topic for which people can cultivate a fear is maths. Yesterday I had a very interesting email from my friend Steve Mildenhall in response to my entry about Andrew Wiles etc. (Memories of the Blair Administration). In that blog I claimed that only a few people in the world were capable of understanding the proof of Fermat's Last Theorem. It turns out that Steve is one of them. This doesn't disprove my assertion, by the way: apart from being extremely smart and hard-working, Steve covered just the type of maths needed in his PhD - and was prepared to spend 3 months doing little other than reading the Wiles proof. In his email Steve noted that his all time favourite maths result is that you can't count the real numbers. One of the beauties of this result is that I can explain it to you.
"Count" means just what you'd expect: mathematicians reassuringly say that a set is countable if you can number the elements, starting with 1 then 2 and so forth. Key point is that you don't have to reach a number where you stop counting for the set to be countable - this describes infinite sets.
Let's put aside for a moment what "real" means here, and why you can't count the real numbers. There are plenty of sets of numbers that you can count. For example, the set of even numbers is countable: 2 is the first, 4 is the second, 6 is the third etc. The set of all positive and negative whole numbers (..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...) is called the integers. While you may think that there are twice as many of these as there are counting numbers (1, 2, 3 etc) it turns out that you can still count them. For example, you can go 0, 1, -1, 2, -2, 3, -3, 4, -4 etc. and every one of the integers will show up on the list that you make.
More surprisingly, the set of all numbers that you can write as a fraction - like 3/4 or 22/7 - is also countable, though this requires a bit more guile to show. First, you have to show a way to lay them all out. A good way way is to make a grid with the numerator (the number on the top of the fraction) along the y-axis and the denominator (the number at the bottom of the fraction) along the x-axis. Then every rational is given by one of the grid points.
Having laid the numbers out on a grid you can count them by starting in the corner and working outwards like this:

The squiggly line gives you the order in which you count the numbers onto your list (if it troubles you that some of these are equal - like 2/2 and 3/3 - you can skip over them after their first appearance).
Well you may wonder if there's anything that you can't count. There is. The numbers like those above that can be expressed as something over something else are called the rationals. In contrast, the entire set of numbers that can be expressed using decimal notation is called (for reasons that you'll be questioning by the end of this blog) the reals. Many people know that pi is an example of a number that can't be expressed precisely as a fraction - 22/7 being an approximation. It's easy to prove that the same is also true of the square root of two. (I wont do it because I'd need to use something that would start to look like an equation.) Now we get to the interesting argument that a mathematician called Cantor found to prove that the reals aren't countable, which runs as follows....
Let's suppose that someone claims that they did find a way to count the real numbers and got them into a list like we did for the evens and the integers. Just to make it concrete, lets assume that the first four numbers in the list are:
something.2451890...
something.7615208...
something.3212122...
something.8734261...
something.4545452...
Cantor pointed out that for any such list you can make another real number that isn't on. Start it with 0. and then set the first digit after the decimal place to be anything that isn't 2 (thus making it different from the first number on the list), the second digit after the decimal to be anything except 6 (thus making it different from the 2nd number), the 3rd digit after the decimal to anything except 1 (thus making it different from the 3rd number) etc etc. Carrying on with this ad infinitum ensures that the number you make isn't the same as any of the numbers on the list, and so the list can't cover all of the reals as claimed.
This is Steve's favourite result - I told you I could explain it! Many of Cantor's contemporaries thought that this was very fishy.
It shows that there's more than one kind of infinity and that in a sense the infinity of the reals (called aleph-1 by mathematicians) is "bigger" than the inifinity of the rationals (called aleph-0). The way that we say this while avoiding saying that one type of infinity is bigger than another (which could sound like nonsense) is to say that aleph-1 has greater cardinality than aleph-0. There is a continuity hypothesis that there aren't any infinities with cardinality between aleph-0 and aleph-1, but there is no known logical proof for this.
When I explained this to Zoe this afternoon (over mint tea and Sprite at the Nejjarine museum) I likened it to when you learn about monkeys: when you're young you know that monkeys are brown hairy animals that swing in the trees. Then when you get older you learn that monkeys come in vervet, squirrel, spider and other types. They all generally have the monkey characteristics that you first learned but there is more nuance than you first appreciated. Same with infinities.
The infinities higher than aleph-0 are really weird. There is a famous result with a geeky name (the Banach-Tarski paradox - Mike said I should mention it) that proves that you can take a "real" sphere, split it into 4 parts and a dot in the middle and then re-assemble it into two spheres each identical to the original. This provides a good hint that the reals aren't real.
Another sign of the weirdness of the reals is to try to find some? Probability tells us that if you pick a number at random on the number line it will, certainly, be a real that's not rational. However, you can easily show that the set of decimal-style numbers for which you can provide an algorithm to say how to determine which digit is at each place of the decimal expansion - or even the wider set of numbers for which you can give any sort of description - is countable. So the uncountability of aleph-1 is provided by numbers for which in principle there can be no description.
There's a lot more that could be said about this but for now I'll hint that the point where it goes funny is where you're allowed to keep making a free choice of the next digit ad infinitum...
Do you find all of this scary, boring or interesting?
This morning I went to get a paper and some vegetables, which is pretty much part of my daily routine, and wore my shorts in the medina for the first time. All the time I was out I didn't see another adult's knees and it felt really uncomfortable; shows how quickly you can fall into the small habits of cultural acclimation.
I read in the paper that the French have voted Non to the "constitution". I never would have expected that. The confusion into which Europe is now propelled will be entertaining and Corsica may be an interesting place from which to watch what happens next - we'll be there at the weekend.
Posted: Wed - June 1, 2005 at 01:04 AM
Quick Links
Links
Archives
XML/RSS Feed
Calendar
| Sun | Mon | Tue | Wed | Thu | Fri | Sat |
Categories
Comments powered by
Statistics
Total entries in this blog:
Total entries in this category:
Published On: Feb 08, 2006 06:20 PM
Total entries in this category:
Published On: Feb 08, 2006 06:20 PM